贝叶斯框架
贝叶斯定理公式如下:
我们把P(A)称为”先验概率”(Prior probability),即在不知道B事件发生的前提下,我们对A事件发生概率的一个主观判断。
P(B|A)/P(B)称为”可能性函数”(Likelyhood),这是一个调整因子,即新信息事件B的发生调整,作用是,使得先验概率更接近真实概率。
P(A|B)称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
因此,贝叶斯定理可以理解成下面的式子:
后验概率(新信息出现后A发生的概率)=先验概率(A发生的概率)×可能性函数(新信息带出现来的调整)
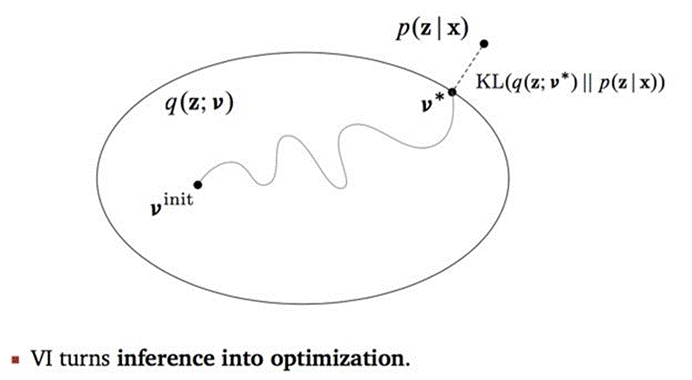
VI(变分推断)
变分推断要解决的问题类,叫做概率机器学习问题。简单来说,专家利用他们的知识,给出合理的模型假设p(z, x),其中包括隐含变量z和观察值变量x(需要说明的是,隐含变量z在通常情况下不止一个,并且相互之间存在依赖关系,这也是问题难求解的原因之一)。我们认为,观察值是从已知的隐含变量组成的层次结构中生成出来的(比如常见的高斯混合模型,隐马尔可夫模型)。
后验概率$p(z | x)$是说,基于我们现有的数据集合x,推断隐含变量的分布情况。根据贝叶斯公式,$p(z|x) = p(z, x) / p(x)$。 我们根据专家提供的生成模型,可知$p(z, x) $部分(可以写出表达式并且方便优化),但是边缘概率$p(x)$,是不能求得的,当$z$连续时,边缘概率需要对所有可能的$z$求积分,不好求。当$z$离散时,计算复杂性随着$x$的增加而指数增长。
我们需要构造$q(z; v)$,并且不断更新$v$,使得$q(z;v)$更接近$p(z|x)$。首先注意,$q(z;v)$的表达,意思是$z$是变量,$v$是$z$的概率分布$q$的参数。所以在构造$q$的时候也分两步,第一,概率分布的选择。第二,参数的选择。第一步,我们在选择$q$的概率分布时,通常会直观选择$p$可能的概率分布,这样能够更好地保证$q$和$p$的相似程度。例如高斯混合模型中,原始假设$p$服从高斯分布,则构造的$q$依然服从高斯分布。之后,我们通过改变$v$,使得$q$不断逼近$p$。
这样一来,一个复杂的推断问题就变成了优化问题。我们只需要优化$p(z|x)$和$q(z|x)$之间的KL散度即可。然而,KL的表达式中依然有一部分不可求的后验概率$p(z|x)$。
当给定数据集后,$P(x)$也就给定了,通过一系列的公式推导,我们可以得到如下公式,其中ELBO中只包括联合概率$p(z, x)$和$q(z; v)$,从而摆脱后验概率。此时最小化KL等价于最大化ELBO(Evidence Lower Bound)。
VAE(Auto-Encoding Variational Bayes)
VAE是和GAN齐名的生成模型,下面我们对VAE的原理进行讲解。
假设我们有一批数据样本$ {X1,…,Xn}$,其整体用$ X $来描述,我们本想根据$ {X1,…,Xn}$ 得到$ X $的分布$ p(X)$,之后便可以根据 $p(X)$ 来采样,就可以得到所有可能的 $X $了(包括 ${X1,…,Xn} $以外的),这是一个终极理想的生成模型。但是直接得到$P(X)$是不可能的,因此我们假设样本$X$的生成过程如下:$p(X)=\sumZp(X|Z)p(Z)$。即,首先由一个先验概率分布$p{\theta^}(Z)$产生隐变量$z^{(i)}$, 然后,样本$x^{(i)}$从条件概率分布$p_{\theta^}(X|Z)$中产生。这是我们的问题就从求$p(X)$变成了求$p(Z)$。
我们首先假设$p{\theta^}(Z)$服从一个(高维的连续的)*标准高斯分布,$p{\theta^}(X|Z)$服从高斯分布(这样的假设具有一定的合理性),其实$p_{\theta^}(Z)$的分布是什么并不重要,这是一个先验概率分布,只是我们的假设,根据上述的贝叶斯理论,我们在先验的基础上通过调整因子得到的后验才是我们关心的。 重要的是如何得到后验概率分布$p{\theta}(Z|X)$,但是根据上述VI中的理论,这时后验概率分布很难求,所以我们使用一个$q{\phi}(Z|X)$来对真实的后验概率分布$p_{\theta}(Z|X)$进行估计。同样根据上述VI中的理论,得到模型的ELBO如下:
在公式中,由于$p(X|Z)$ 形如Decoder,$q(Z|X)$形如Encoder,所以称为VAE。
由 Encoder 得到隐变量 z 的过程需要保证是连续的,这样才可以使用基于梯度的方法进行优化,如果设计 Encoder 的输出为多元正态分布的参数$\mu(X)$和$\sum(X)$,那么从分布$N(\mu(X),\sum(X))$中采样$z$的操作破坏了连续性。因此,这里我们使用一个叫做重参化的技巧来保证连续性,使用如下方法代替采样:
其中$\epsilon$服从标准正态分布。
所以整个VAE训练中的模型结构如下所示:
我们试着解释一下VAE的优化目标:
期望部分可以看作是encoder和decoder的部分,可以看作真正的目标函数,也就是经过编码再解码之后得到的数据尽量和样本相像。
而KL散度部分可以看作一个正则化项,即Z的后验分布要尽可能的接近一个标准正态分布,避免模型退化成普通的Auto-Encoder。
测试时我们只需要Decoder就可以了。由于目标函数中的 KL 散度已经把后验分布和先验分布拉近,z 可以从先验采样。