MCMC
MCMC命名
MCMC由两个MC组成,即马尔可夫链和蒙特卡罗方法。
MCMC方法解决的问题
蒙特卡罗原来是一个赌场的名称,用它作为名字大概是因为蒙特卡罗方法是一种随机模拟的方法,这很像赌博场里面的扔骰子的过程。最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。比如积分:
$\theta=\int_a^b f(x)dx$
如果我们很难求解出$f(x)$的原函数,那么这个积分比较难求解。这时我们可以通过蒙特卡罗方法来模拟求解近似值。
$\theta=\inta^b f(x)dx=\int_a^b {f(x)\over p(x)}p(x)dx=E{x-p(x)}[{f(x)\over p(x)}]$
即,把$q(x)$看作是x在区间内的分布函数,分数部分看作一个函数,然后求函数$f(x)\over q(x)$在分布$q(x)$下的期望。如果此时我们从$q(x)$中采样n个点,就可以使用以下公式近似
$\theta=\inta^b f(x)dx=\int_a^b {f(x)\over p(x)}p(x)dx=E{x-p(x)}[{f(x)\over p(x)}]\approx{1\over n}\sum_{i=1}^n {f(x)\over p(x)}(其中x是从p(x)中采样的点)$
这时我们的问题就变成了如何从$p(x)$中采样n个样本点。MCMC就是用来解决这个问题的
采样
常见概率分布采样
均匀分布 :
一般通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本
其他常见分布:
比如正态分布,t分布,F分布,Beta分布,Gamma分布可以从均匀分布得到的采样样本转化得到。python中提供了类库可以直接生成对应分布的样本。
非常见概率分布采样
接受拒绝采样
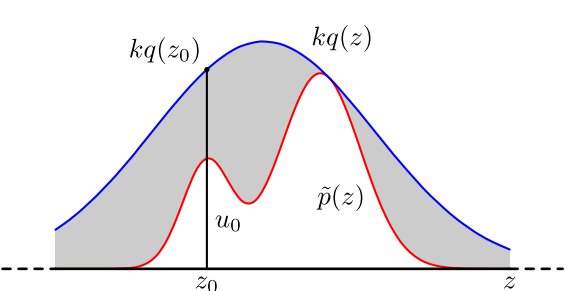
既然 $p(x)$ 太复杂在程序中没法直接采样,那么我设定一个程序可采样的分布 $q(x)$ 比如高斯分布,然后按照一定的方法拒绝某些样本,以达到接近$ p(x)$ 分布的目的,其中$q(x)$叫做 proposal distribution。
具体采用过程如下,设定一个方便采样的常用概率分布函数 $q(x)$,以及一个常量 $k$,使得 $p(x)$总在 $kq(x)$的下方。
因为$q(x)$是正态分布,我们可以方便的从中采样。之后,从均匀分布$ (0,kq(x))$中采样得到一个值$u$,如果$u$落在了上图中的灰色区域,则拒绝这次抽样,否则接受这个样本$z_0$
缺点:找到合适的$q(x)$和$k$有时比较困难,有时也很难写出$p(x)$的分布
MCMC采样
马尔可夫链的收敛性质
一个马尔可夫链即使有不同初始概率分布,在状态转移矩阵不变的情况下,最终状态的概率分布趋于同一个稳定的概率分布, 也就是说我们的马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。
根据这个性质,可以这样说,如果我们得到了某个平稳分布对应的马尔可夫链状态转移矩阵,就可以从马尔可夫链中采样出来。
马尔可夫链的收敛条件
如果非周期马尔科夫链的状态转移矩阵$P$和概率分布$π(x)$对于所有的$i,j$满足:
$π(i)P(i,j)=π(j)P(j,i)$则称概率分布$π(x)$是状态转移矩阵$P$的平稳分布。
这其实很好理解,也就是说根据这个状态转移矩阵,到最后各个状态之间的转移到达一种平衡,有多少的A转移成B,就有多少的B转移成A
从马尔可夫链中采样
- 基于一个可采样的简单概率分布$\pi_0(x)$采样得到$x_0$,基于条件概率分布$P(x|x_0)$采样状态$x_1$ ,一直进行下去
- 取出马尔可夫链收敛后的采样集
所以我们的问题现在变成了如何获取一个平稳分布对应的状态转移矩阵
由于一般情况下,目标平稳分布$π(x)$和某一个马尔科夫链状态转移矩阵$Q$不满足细致平稳条件,即$π(i)Q(i,j)\not=π(j)Q(j,i)$
我们可以对上式做一个改造,使细致平稳条件成立。方法是引入一个$α(i,j)$,使上式可以取等号,即$π(i)Q(i,j)\alpha(i,j)=π(j)Q(j,i)\alpha(j,i)$,
其中$\alpha(i,j)=π(j)Q(j,i)$,$\alpha(j,i)=π(i)Q(i,j)$
所以状态转移概率矩阵$P(i,j)=Q(i,j)\alpha(i,j)$
在这个公式中,$Q(i,j) $是我们随便取的,$\alpha(j,i)$是由平稳分布$π(j)$和$Q(i,j) $算出来的,所以这个$P(i,j)$是可求的。
$α(i,j)$我们有一般称之为接受率。取值在[0,1]之间,可以理解为一个概率值。即目标矩阵$P$可以通过任意一个马尔科夫链状态转移矩阵$Q$以一定的接受率获得。 这和接受拒绝采样的思路是一样的。
缺点:$α(i,j)$可能非常小,导致大部分情况下拒绝转移,这时马尔可夫链很难收敛
M-H采样
M-H采样是Metropolis-Hastings采样的简称,这个算法首先由Metropolis提出,被Hastings改进,因此被称之为Metropolis-Hastings采样或M-H采样。
我们再来分析一下MCMC:
$π(i)Q(i,j)\alpha(i,j)=π(j)Q(j,i)\alpha(j,i)$,
$α(i,j)$可能非常小比如为0.1,而$α(j,i)$为0.2
$π(i)Q(i,j)×0.1=π(j)Q(j,i)×0.2$
如果两边同时扩大五倍,接受率提高到了0.5,但是细致平稳条件却仍然是满足的,即
$π(i)Q(i,j)×0.5=π(j)Q(j,i)×1$
这样我们的接受率可以做如下改进,即:
$α(i,j)=min{ {π(j)Q(j,i)\over π(i)Q(i,j)},1}$
缺点: 由于$α(i,j)$ 计算式的存在,在高维时计算量大,并且由于接受率的原因导致算法收敛时间变长。二是有些高维数据,特征的条件概率分布好求,但是特征的联合分布不好求。
Gibbs采样
在M-H采样中我们通过引入接受率使细致平稳条件满足。现在我们换一个思路。我们发现,在高维的情况下,比如在二维的情况下
在$x_1=x^{(1)}_1$这条直线上,如果用条件概率分布$π(x_2|x^{(1)}_1)$作为马尔科夫链的状态转移概率,则任意两个点之间的转移满足细致平稳条件!
因而我们可以构造处一个状态转移矩阵