训练误差的来源
where does the error come from?
Error comes from bias and variance.
| bias | variance | 常见误差 | |
|---|---|---|---|
| 复杂模型 | 较小 | 较大 | overfiting |
| 简单模型 | 较大 | 较小 | underfiting |
Tips for training DNN
啥也不说,先看张图
New activation function
对激活函数进行创新可以改进模型
question:为什么需要激活函数?
如果没有激活函数,整个网络就是线性的,线性的缺点,在于线性函数的组合仍然是线性函数,这意味着无论我们堆多少层网络,如果这些层都使用线性激活函数,那么这些层最终等效于一层。(可以自己画一个简单的全连接网络计算一下)
常见激活函数
Sigmoid![微信截图_20200216012819 微信截图_20200216012819]()
生物神经元似乎是用 Sigmoid(S 型)激活函数活动的,因此研究人员在很长一段时间内坚持 Sigmoid 函数。但事实证明,Relu 激活函数通常在 ANN 工作得更好。这是生物研究误导的例子之一。
当神经网络有很多层,每个隐藏层都使用Sigmoid函数作为激励函数时,很容易引起梯度消失的问题
我们知道Sigmoid函数有一个缺点:当x较大或较小时,导数接近0;并且Sigmoid函数导数的最大值是0.25
我们将问题简单化来说明梯度消失问题,假设输入只有一个特征,没有偏置单元,每层只有一个神经元
则代价函数对w的导数可以表示为:
如果我们使用标准方法来初始化网络中的权重,那么会使用一个均值为0标准差为1的高斯分布。因此所有的权重通常会满足|wj|<1,而s‘是小于0.25的值,那么当神经网络特别深的时候,梯度呈指数级衰减,导数在每一层至少会被压缩为原来的1/4,当z值绝对值特别大时,导数趋于0,正是因为这两个原因,从输出层不断向输入层反向传播训练时,导数很容易逐渐变为0,使得权重和偏差参数无法被更新,导致神经网络无法被优化,训练永远不会收敛到良好的解决方案。 这被称为梯度消失问题。
当我们将w初始化为一个较大的值时,例如>10的值,那么从输出层到输入层每一层都会有一个s‘(zn)×wn的倍增,当s‘(zn)为0.25时,s‘(zn)×wn>2.5,同梯度消失类似,当神经网络很深时,梯度呈指数级增长,最后到输入时,梯度将会非常大,我们会得到一个非常大的权重更新,这就是梯度爆炸的问题,在循环神经网络中最为常见。
原文链接:https://blog.csdn.net/junjun150013652/article/details/81274958
ReLU
ReLU可以解决Sigmoid函数的梯度消失和梯度爆炸问题。
question:ReLU化简后不就是线性激活函数吗?
关于这个问题,可以有以下解释:
1、首先什么是线性的网络,如果把线性网络看成一个大的矩阵M。那么输入样本A和B,则会经过同样的线性变换MA,MB(这里A和B经历的线性变换矩阵M是一样的)。
2、的确对于单一的样本A,经过由relu激活函数所构成神经网络,其过程确实可以等价是经过了一个线性变换M1,但是对于样本B,在经过同样的网络时,由于每个神经元是否激活(0或者Wx+b)与样本A经过时情形不同了(不同样本),因此B所经历的线性变换M2并不等于M1。因此,relu构成的神经网络虽然对每个样本都是线性变换,但是不同样本之间经历的线性变换M并不一样,所以整个样本空间在经过relu构成的网络时其实是经历了非线性变换的。
3、还有一种解释就是,不同样本的同一个feature,在通过relu构成的神经网络时,流经的路径不一样(relu激活值为0,则堵塞;激活值为本身,则通过),因此最终的输出空间其实是输入空间的非线性变换得来的。
4、更极端的,不管是tanh还是sigmoid,你都可以把它们近似看成是分段线性的函数(很多段),但依然能够有非线性表达能力;relu虽然只有两段,但同样也是非线性激活函数,道理与之是一样的。
链接:https://www.jianshu.com/p/66cb257ec37e
Leaky ReLU
Maxout
question:Maxout激活函数如何求导?
根据Maxout将网络化简后,去掉那些不参与正向传播过程的神经单元,再进行求导。
同理CNN中的pooling层也这样求导。
Adaptive Learning Rate
At the beginning,we are far from the destination,so we use large learning rate.
After several epochs,we are close to the destination,so we reduce the learning rate.
1/t decay
Adagrad
依然符合随着训练次数增加,learning rate减小。
question:当某一次grad很大时,学习率反而更小了,这难道不和我们的规律矛盾吗?
确实有这样反直觉的疑惑,一种合理的解释是:root mean square of the previous derivatives of the parameter w 其实代表了w的二次微分,即陡峭程度,用w的一次微分除以二次微分,才是w应该更新的最佳步长。
RMSProp
error surface can be very complex when trainning NN,所以learning rate应该具备快速变化的能力。
可以参照计算机网络RTT更新公式。
Momentum
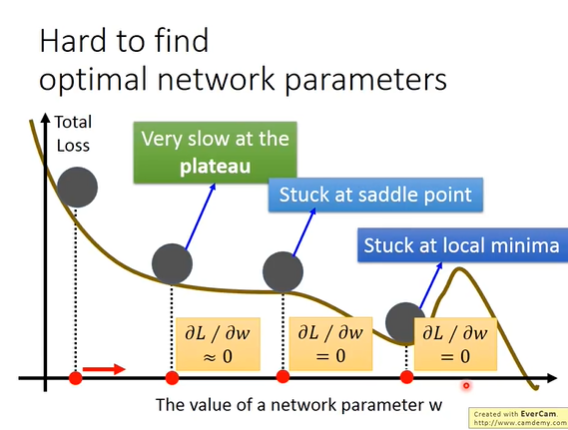
在网络训练中,loss可能收敛在plateau,saddle point, local minima.可以参照物理学中的知识,加一个momentum。
不加momentum
加momentum
Adam
RMSProb+Momentum
接下来的方法都是处理过拟合的方法
Early Stopping
没什么卵用
Regularization
L2正则化
使用L2范数做正则化,每次会使Weight小一点,所以这也叫做weight decay。
正则化这个tip相较于其他tip对网络的优化程度比较小。解释如下:
我们在训练神经网络时,通常对w初始化一个比较接近0的数,然后通过一次次更新,w距离0越来越远。而正则化所做的事情,其实就是每次使w离0近一点,这难道不就相当于减少训练次数吗?
L1正则化
sgn()为正负1,当w为正,则结果-1,w为负,则结果加1。
L1正则化和L2正则化对比:
L1 learn出来的值有的很大,有的很小,分布很散,因为他每次都是加减固定的值。而L2 learn出来的值都偏小,因为他是成比例缩小的。
Dropout
Why the weigth should multiply (1-p) when testing?
来一个直观的解释,假设现在有100个1,dropout rate 是20%,那么只有80个1参与运算,sum之后值为80,当测试时,100个1全部参与运算,所以每个1都要乘以80%,再sum,才能得到80。
Dropout is a kind of ensemble